Tras construir el primer prototipo, me di cuenta de que los perfiles rectangulares de aluminio del chatarrero no eran lo bastante estables y dejaban demasiado juego. Por eso decidí sustituirlos por tubos suficientemente estables.
Haga clic aquí para ver Parte 1.
Diseño de tubos de aluminio
El aluminio es un material valioso cuya producción requiere mucho trabajo y energía. Para no desperdiciar nada, quería asegurarme de que el material que encargaba era lo bastante resistente. Esta vez no me limité a confiar en mi intuición, sino que hice cálculos aproximados de la rigidez a la flexión y a la torsión. Para esto, me concentré en la pieza en Y, que probablemente estaría sometida a la mayor carga. Basándome en mi intuición, reduje la selección de posibles perfiles para la pieza en Y a cuatro secciones de tubo redondo diferentes (perfil A-D).
| Perfil | Diámetro exterior | Grosor de la pared |
|---|---|---|
| A | 40 mm | 2 mm |
| B | 30 mm | 2.5 mm |
| C | 35 mm | 2 mm |
| D | 50 mm | 2 mm |
Para cada perfil calculé los esfuerzos de flexión y torsión previstos y los comparé con los límites admisibles para el aluminio.
Advertencia matemática: Si los números y las fórmulas no son lo tuyo, pasa a la siguiente sección.
Dado que mis conocimientos de mecánica son ya un poco antiguos, para todos los cálculos utilicé las herramientas en línea del siguiente sitio web https://www.johannes-strommer.com/. Me abstendré de reconstruir las operaciones de cálculo en esta entrada del blog.
Material
Los tubos solicitados están fabricados con el material AlMgSi0,5. La tabla siguiente resume los datos clave del material:
R_{\text{m, min}} |
R_{\text{p0.2, min}} |
A_{\text{min}} |
A_{50} |
\rho |
|---|---|---|---|---|
| 215 | 160 | 8 | 6 | 2700 |
El esfuerzo máximo de tracción se calcula alternativamente con el límite elástico y un factor de seguridad de 1.6.
\frac{R_{p0,2, min}}{1.6} = 100 \frac{N}{mm^2}
Tensiones de flexión
El siguiente dibujo muestra la hipótesis de carga simplificada que he utilizado para calcular las tensiones de flexión.
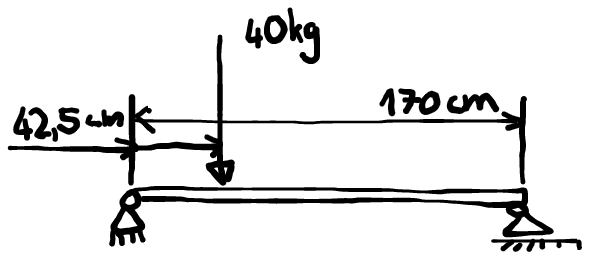
Este supuesto de carga se pudo transferir 1:1 en el sitio web de Johanes Strommer. Los resultados de los cálculos se resumen en la tabla.
| Perfil | Tensión máx. de flexión | Flexión máx. |
|---|---|---|
| A | \sigma_{max} = 57.9 \frac{N}{mm^2} |
f_{max} = 9.28 mm |
| B | \sigma_{max} = 91.1 \frac{N}{mm^2} |
f_{max} = 19.48 mm |
| C | \sigma_{max} = 77.2 \frac{N}{mm^2} |
f_{max} = 14.14 mm |
| D | \sigma_{max} = 35.2 \frac{N}{mm^2} |
f_{max} = 4.60 mm |
Tensiones de torsión
En la siguiente imagen se muestra el supuesto de carga, que se transfirió a la herramienta en línea de Johanes Strommer.

Los resultados de los cálculos se resumen en el tabla.
| Perfil | Tensión máx. de torsión | Tensión máx. de cizalladura |
|---|---|---|
| A | \tau_{t, max} = 72.6 \frac{N}{mm^2} |
\tau_{s, max} = 1.6 \frac{N}{mm^2} |
| B | \tau_{t, max} = 114.4 \frac{N}{mm^2} |
\tau_{s, max} = 1.8 \frac{N}{mm^2} |
| C | \tau_{t, max} = 97.0 \frac{N}{mm^2} |
\tau_{s, max} = 1.9 \frac{N}{mm^2} |
| D | \tau_{t, max} = 45.1 \frac{N}{mm^2} |
\tau_{s, max} = 1.3 \frac{N}{mm^2} |
Resumen
La siguiente tabla resume los resultados de los cálculos. Los puntos verdes indican una resistencia suficiente, los amarillos los casos límite y los rojos la falta de resistencia.
| Perfil | Esfuerzo de flexión | Deformación | Torsión | Peso / m | Coste / m |
|---|---|---|---|---|---|
| A | 🟢 | 🟢 | 🟢 | 645 g | 9,80 € |
| B | 🟡 | 🟢 | 🔴 | 583 g | 8,99 € |
| C | 🟡 | 🟢 | 🟡 | 559 g | 8,52 € |
| D | 🟢 | 🟢 | 🟢 | 815 g | 13,08 € |
Basándome en estos cálculos y sopesando el precio y el peso, me decidí por el perfil A con un diámetro exterior de 40 mm.
Cinta de transporte
La entrega de los deseados tubos de aluminio se hizo esperar y me estaba aburriendo. Por eso empecé a coser una cinta de transporte que me facilitara sujetar el remolque de senderismo durante las caminatas. Con una máquina de coser, hilo superior demasiado fino y mi vieja espalda de senderismo empecé. Cabe mencionar de entrada que apenas tengo experiencia en costura. Para enhebrar el hilo superior y subir el hilo inferior, tuve que estudiar las instrucciones durante una buena hora. Una vez hecho esto, deshice las costuras que unen el cinturón de cadera y las trabillas de los hombros con el resto de la espalda. A continuación, cosí una pieza en forma de T a partir de un trozo de cinta, que luego cosí a las trabillas de los hombros y al cinturón de cadera.
Todo fue bastante fácil, pero el hilo superior se rompió aproximadamente cada 3 cm de costura y acabé pasando casi 3 días en la acción. Durante este tiempo volví a enhebrar el hilo superior cientos de veces. Definitivamente ahora soy bastante hábil en eso. Compensé la falta de grosor del hilo cosiendo todas las costuras al menos el doble, si no el triple.
En general, la cinta da una impresión sólida y estoy bastante contento de haber podido transformar mi vieja y rota bolsa de viaje en algo útil.
 |
 |
Alumania
A principios de marzo llegaron por fin los tubos de aluminio encargados. El 2 de marzo me encerré en el taller y corté los tubos a las longitudes adecuadas. Por desgracia, tuve que darme cuenta una vez más de que cortar con una amoladora angular no es muy preciso. La junta de la pieza en Y está cortada bastante mal. Espero poder cerrar los huecos al soldar. Para soldar aluminio se necesita un equipo especial (MIG o TIG), que no tenemos en el taller en mi casa. Afortunadamente, hay un taller abierto no muy lejos de nosotros donde se puede soldar aluminio. He concertado una cita allí y prepararé todo para soldar hasta entonces.
Corte de tubos
Primero calculé las longitudes de los bordes cortados que necesitaría para obtener los ángulos deseados. Para ello, apliqué las funciones trigonométricas básicas (sin, cos y tan).

Luego marqué los bordes cortados con un lápiz rojo. Utilicé una regla flexible, una escuadra, un calibre y una escuadra de mecánico. Por desgracia, ninguna de estas herramientas era realmente adecuada.

Por último, corté los tubos a lo largo de las marcas con la amoladora angular.

Asas telescópicas
Para hacer las asas telescópicas, empecé cortando en ángulo los extremos. Como soporte para las varillas roscadas utilicé un trozo de madera redonda de 30 cm que me había sobrado, que corté en trozos de unos 2-3 cm, en cada uno de los cuales taladré un agujero de 6 mm.

Para fijar las varillas roscadas a los trozos de tubo inclinados, sujeté cada una con un soporte de madera con dos tuercas de tope y arandelas estriadas (de una vieja bicicleta). El resultado se puede ver en la foto de abajo.

Para evitar que los cojinetes de madera patinaran, taladré un agujero de 3 mm a través del tubo de aluminio y hasta la mitad del cojinete de madera. A continuación, corté una rosca de 4 mm en el tubo de aluminio y atornillé el tornillo prisionero correspondiente.


En el extremo delantero de las asas telescópicas se puede enroscar una tuerca con una arandela más ancha que el tubo. Al apretar la tuerca, la pieza inclinada del tubo se desplaza hacia delante y se encaja. Esto permite extender y retraer la barra telescópica y bloquearla a la longitud deseada. El resultado de la jornada de taller puede verse en la siguiente imagen.

La construcción del asa del remolque de senderismo está casi terminada. Aún faltan los cordones de soldadura que unen los tubos.
